KMP （Knuth-Morris-Pratt）算法是一种字符串查找算法。本文对该算法做一些整理，用来提醒以后的自己。

原理

KMP 算法主要利用被匹配字符串的相同前缀和后缀，来减少回溯成本。

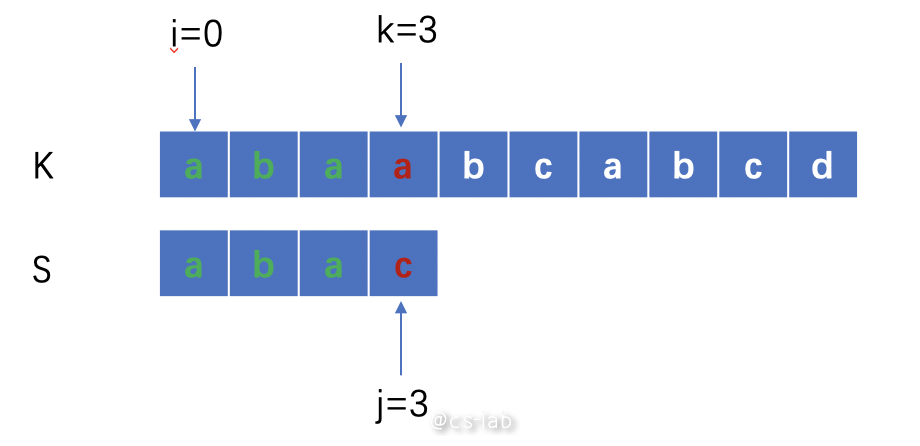
比如基础字符串 K 和匹配字符串 S，最简单也是复杂度最高的算法如下：

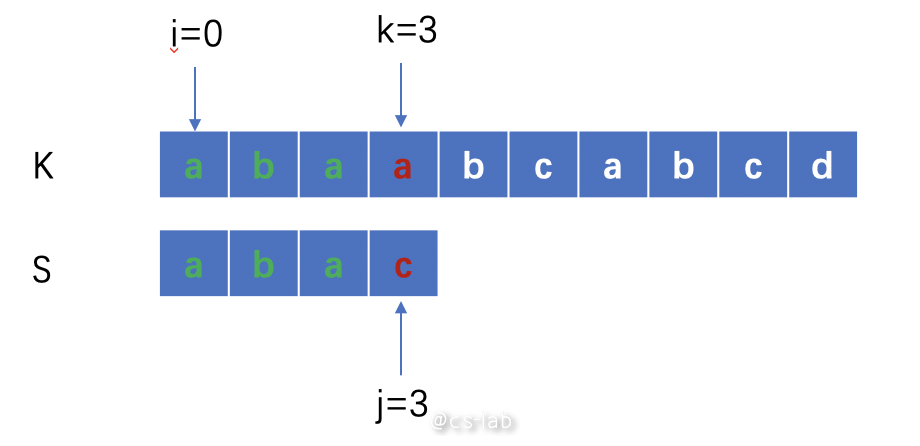
当索引逐渐后移，遇到不匹配的一项时，需要将索引 i 向前移动一位，k 初始化成 i，j 回退到 0：

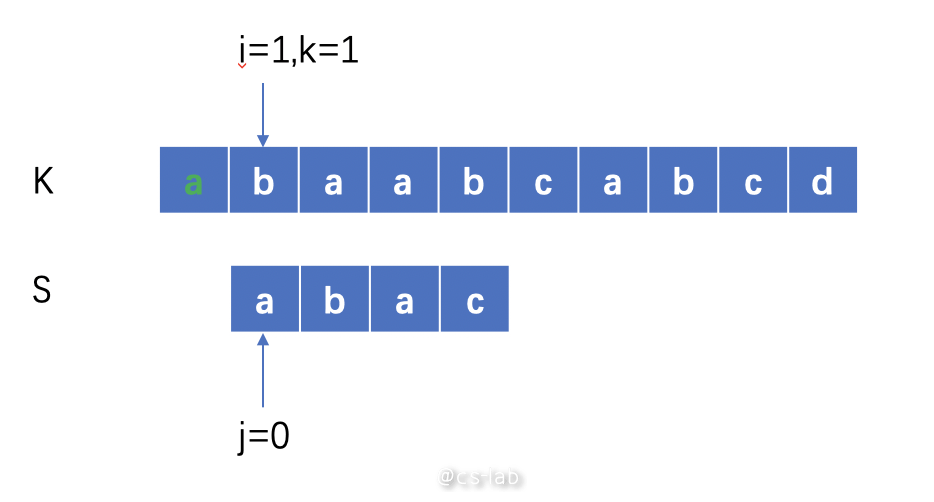
这样做的缺点显而易见：第一次匹配过的几位全是浪费，在第二次匹配的时候完全作废，所以增加了时间复杂度。

而相同的情况，KMP 的解法是只需要两个索引 i 和 j，且只需要回溯 j，也就是说，可以利用匹配字符串自身的特性来决定下一次匹配从第几位开始即可。

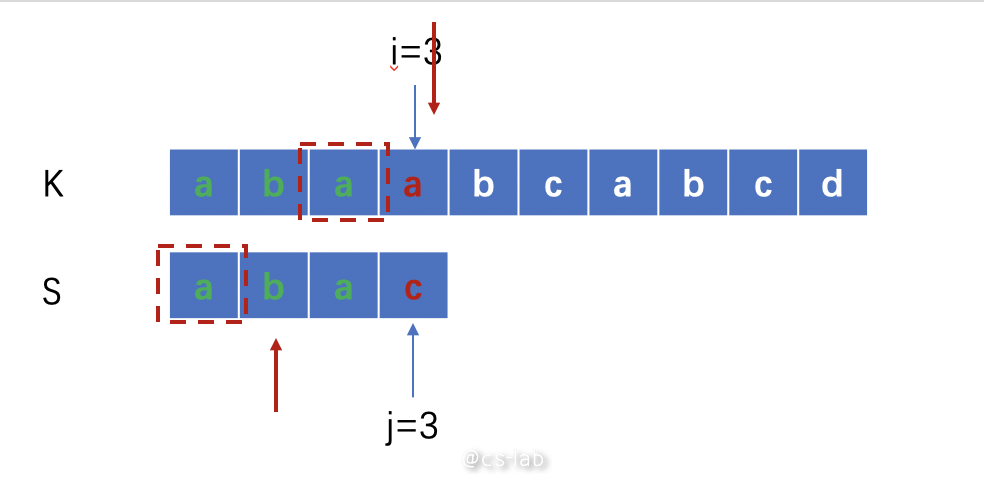
上图中，在选择下一次匹配点的时候，可以看到 K 中前面已匹配过的地方，红框框中的 "a" 和 K 中的红框框的 "a" 相等，所以可以选下一位即 j=1 作为下一个匹配点。可以看到其实是因为，在前面的安全（已匹配）字符串中最大相同前缀后缀为 "a"，所以可以将 j 回溯到前缀后一位，如下：

利用这个特性，可以快速提高字符串匹配效率，而每一次的回溯点是 KMP 算法的关键，即 next 数组。

next 数组

next 数组有两种构建方式。

第一种是每一位表示当前可回溯点（特点是第 0 位为 -1）。原理是若 j 位的数与 i 位的相同，则 next 的 i+1 位为 j+1；若 j 位的数与 i 位的不同，则将 j 回溯到 next 数组中第 j 位记录的数值，重新比较。原理图如下：

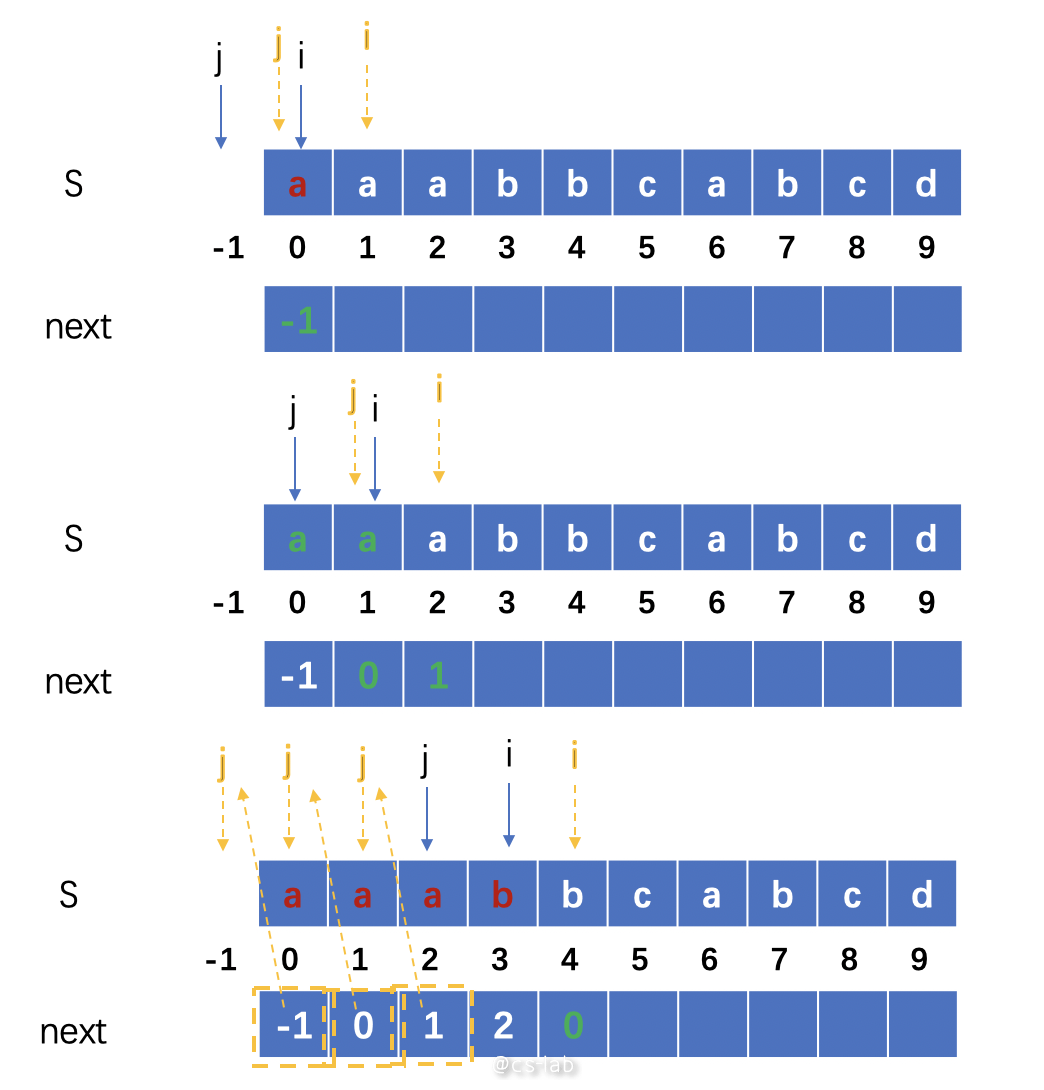
这种构建方法用 Golang 表达出来：

func nextArry(needle string) []int {
	i := 0
	j := -1
	var next = make([]int, len(needle)+1)
	next[0] = -1
	for ; i < len(needle); {
		if j == -1 || needle[i] == needle[j] {
			j++
			i++
			next[i] = j
		} else {
			j = next[j]
		}
	}
	return next
}

第二种是每一位表示当前位数向前的前缀字符串（特点是第 0 位为 0），其最大相同前后缀的位数，用来在 KMP 算法中找到可回溯的位置。原理是若 j 位的数与 i 位的相同，则 next 的 i 位为 j+1；若 j 位的数与 i 位的不同，则将 j 回溯到 next 数组中第 j-1 位记录的数值，重新比较。原理图如下：

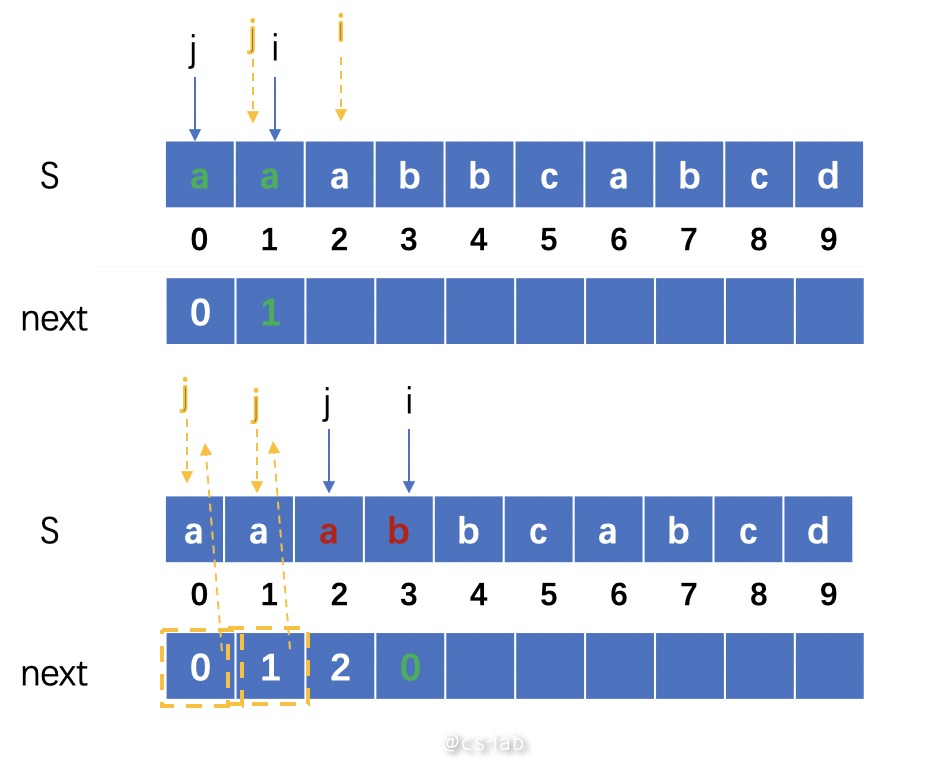
这种构建方法用 Golang 表达出来：

func nextArry(needle string) []int {
	i := 1
	j := 0
	var next = make([]int, len(needle))
	next[0] = 0
	for ; i < len(needle); {
		if needle[i] == needle[j] {
			j++
			next[i] = j
			i++
		} else if j == 0 {
			i++
		} else {
			j = next[j-1]
		}
	}
	return next
}

KMP 算法

next 数组构建出来，字符串匹配就好办了，每次匹配到不一样的字符时，只需根据 next 数组回溯 j 即可。显然，整个字符串匹配算法的时间复杂度被降到了 O(m+n)。

针对第一种 next 数组的构建方法，KMP 算法：

func strStr(haystack string, needle string) int {
	if len(needle) == 0 {
		return 0
	}
	if len(haystack) < len(needle) {
		return -1
	}
	var next = nextArry(needle)
	var isFound = false
	i, j := 0, 0
	for ; i < len(haystack); {

		if j == -1 || haystack[i] == needle[j] {
			j++
			i++
		} else {
			j = next[j]
		}
		if j == len(needle) {
			isFound = true
			break
		}
	}

	if isFound {
		return i - j
	}
	return -1
}

针对第二种 next 数组的构建方法，KMP 算法：

func strStr(haystack string, needle string) int {
	if len(needle) == 0 {
		return 0
	}
	if len(haystack) < len(needle) {
		return -1
	}
	var next = nextArry(needle)
	var isFound = false
	i, j := 0, 0
	for ; i < len(haystack); {
		if haystack[i] == needle[j] {
			j++
			i++
		} else if j == 0 {
			i++
		} else {
			j = next[j-1]
		}
		if j == len(needle) {
			isFound = true
			break
		}
	}

	if isFound {
		return i - j
	}
	return -1
}